Volatility Surface
We're going to use Python to generate an implied volatility surface for a family of options contracts. This is an extremely common tool for analyzing options and is a key component of many quantitative trading strategies.
The Black-Scholes model is like a recipe for pricing options - it takes ingredients like the current stock price, strike price, time until expiration, interest rates, and volatility, and spits out what an option should theoretically cost. But in the real world, traders often work backwards - they look at actual market prices of options and try to figure out what volatility number would make the Black-Scholes formula give that price. This reverse-engineered number is called the implied volatility or IV. Think of implied volatility as the market's forecast of how much a stock might bounce around in the future. Higher IV means traders expect bigger price swings (and are willing to pay more for options as insurance), while lower IV suggests they expect smoother sailing ahead. It's like a fear gauge - when investors are nervous about the future, they'll pay more for options protection, driving up IVs.
What makes this really interesting is that options with different strike prices and expiration dates often have different IVs, even for the same underlying stock. When you plot these IVs, you get what's called the volatility surface - a 3D visualization that shows how the market's expectations of future volatility vary across strikes and time. This surface often shows patterns like the volatility smile or volatility skew, where out-of-the-money puts have higher IVs than calls, reflecting the market's tendency to worry more about crashes than rallies. And we can use this surface to identify inefficiencies and arbitrage opportunities.
In order to generate the volatility surface, we need to install a few libraries. These are mostly standard except for the py_vollib library which is a Python wrapper for the VolLib library for doing efficient Black-Scholes calculations.
pip install numpy pandas seaborn matplotlib py_vollib
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import scipy.interpolate as interpolate
import py_vollib.black_scholes.implied_volatility as iv
from py_vollib.black_scholes import black_scholes as bs
Now we need to load the price data for the underlying asset and the strike data for the options chain. In practice we would load this data from Bloomberg or some other vendor. But for now we'll just load it from CSV files. The data consits of a chain of options contracts for the underlying asset SPY. We have the strike price, price, and expiration date for each contract. From this we can use the Black-Scholes formula to calculate the implied volatility for each contract.
| contractSymbol | lastTradeDate | strike | lastPrice | inTheMoney | currency | optionType | expiration | daysToExpiration |
|---|---|---|---|---|---|---|---|---|
| SPY241227C00598000 | 2024-11-26 20:57:08+00:00 | 598.0 | 10.0 | True | USD | call | 2024-12-27 23:59:59 | 31 |
| SPY241227C00599000 | 2024-11-26 21:08:56+00:00 | 599.0 | 9.4 | True | USD | call | 2024-12-27 23:59:59 | 31 |
| SPY241227C00600000 | 2024-11-26 21:11:54+00:00 | 600.0 | 8.8 | True | USD | call | 2024-12-27 23:59:59 | 31 |
| SPY241227C00601000 | 2024-11-26 20:50:47+00:00 | 601.0 | 8.06 | False | USD | call | 2024-12-27 23:59:59 | 31 |
| SPY241227C00602000 | 2024-11-26 20:57:59+00:00 | 602.0 | 7.39 | False | USD | call | 2024-12-27 23:59:59 | 31 |
| SPY241227C00602500 | 2024-11-26 21:00:20+00:00 | 602.5 | 7.05 | False | USD | call | 2024-12-27 23:59:59 | 31 |
Recall that the Black-Scholes formula for a call option is given by:
$$
C = S \cdot N(d_1) - K \cdot e^{-rT} \cdot N(d_2) \
$$
$$
d_1 = \frac{\ln(S/K) + (r + \sigma^2/2)T}{\sigma\sqrt{T}},\quad d_2 = d_1 - \sigma\sqrt{T}
$$
where:
- \(C\) is the price of the call option
- \(S\) is the current price of the underlying asset
- \(K\) is the strike price of the option
- \(r\) is the risk-free interest rate (i.e. the yield on a 3-month US Treasury bill)
- \(\sigma\) is the volatility of the underlying asset
- \(T\) is the time until expiration
- \(N(x)\) is the cumulative distribution function of the standard normal distribution
Out of Black-Sholes we get the concept of moneyness that describes the relationship between the current price of the underlying asset and the strike price of the option. An option is considered in the money (often abbreviated ITM or the opposite which is OTM or out of the money) when it has intrinsic value, meaning that exercising the option would lead to a positive cash flow. For call options, this occurs when the strike price is lower than the current market price of the underlying asset, allowing the holder to buy the asset at a lower price than its market value. Conversely, for put options, an option is ITM when the strike price is higher than the current market price, enabling the holder to sell the asset at a price greater than its market value.
- In-the-Money (ITM): Options that have intrinsic value. For calls, the strike price is below the current market price; for puts, it's above.
- At-the-Money (ATM): Options where the strike price is approximately equal to the current market price of the underlying asset.
- Out-of-the-Money (OTM): Options that have no intrinsic value. For calls, this means the strike price is above the current market price of the underlying asset; for puts, it's below.
ITM options typically have higher premiums due to their intrinsic value, making them more desirable for traders who anticipate further favorable movements in the underlying asset's price. Grossly, the risk associated with ITM options is also higher, as they can be more sensitive to changes in market conditions. And generally OTM options are cheaper but have a higher probability of expiring worthless.
We plug our market data into the Black-Scholes formula to calculate the implied volatility for each option in the chain. For the risk-free rate we use the yield on a 3-month US Treasury bill, replace this with the actual risk-free rate at present for the option you are analyzing.
def get_current_market_data():
spy_price = pd.read_csv(PRICE_CSV)
current_price = spy_price["Close"].iloc[-1]
risk_free_rate = 4.3 / 100 # 3-month Treasury yield (4.3% as of 2024-11-27)
return risk_free_rate, spy_price, current_price
def calculate_iv(row, risk_free_rate, sigma):
try:
price = bs(
S=row["lastPrice"],
K=row["strike"],
t=row["t"],
r=risk_free_rate,
sigma=sigma,
flag="c",
)
return iv.implied_volatility(
price=price,
S=row["lastPrice"],
K=row["strike"],
t=row["t"],
r=risk_free_rate,
flag="c",
)
except:
print(f"Error calculating IV for {row['strike']}")
return np.nan
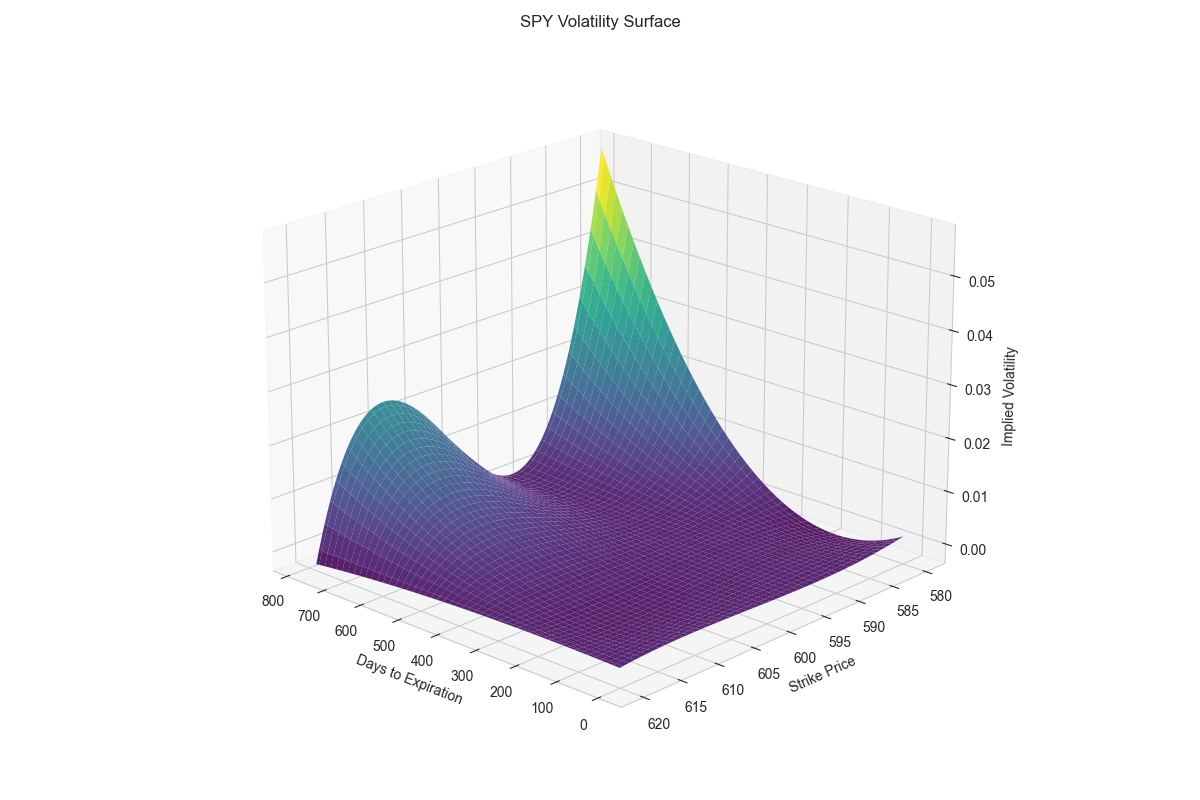
The volatility surface is a three-dimensional representation of implied volatility across different strike prices and expiration dates. It provides a comprehensive view of how the market prices options across various strikes and maturities, revealing important patterns in market expectations and risk preferences. In a perfect theoretical Black-Scholes world, this surface would be completely flat, as volatility would be constant across all strikes and expirations. However, in reality, we observe various patterns and distortions in the surface.
To construct a smooth and continuous volatility surface from discrete market data, we employ interpolation techniques. In our implementation, we use a bivariate spline interpolation method through SciPy's SmoothBivariateSpline. This approach fits a smooth surface through our observed implied volatility points while maintaining a balance between accuracy and smoothness. The smoothing parameter (s=0.1) controls how closely the surface fits the original data points - a smaller value creates a tighter fit to the data, while a larger value produces a smoother surface that might be less sensitive to market noise.
def create_volatility_surface(calls_data):
surface = (
calls_data[["daysToExpiration", "strike", "impliedVolatility"]]
.pivot_table(
values="impliedVolatility", index="strike", columns="daysToExpiration"
)
.dropna()
)
# Prepare interpolation data
x = surface.columns.values
y = surface.index.values
X, Y = np.meshgrid(x, y)
Z = surface.values
# Create interpolation points
x_new = np.linspace(x.min(), x.max(), 100)
y_new = np.linspace(y.min(), y.max(), 100)
X_new, Y_new = np.meshgrid(x_new, y_new)
# Perform interpolation
spline = interpolate.SmoothBivariateSpline(
X.flatten(), Y.flatten(), Z.flatten(), s=0.1
)
Z_smooth = spline(x_new, y_new)
return X_new, Y_new, Z_smooth
def plot_volatility_surface(X, Y, Z):
plt.style.use("default")
sns.set_style("whitegrid", {"axes.grid": False})
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(
X, Y, Z, cmap="viridis", alpha=0.9, linewidth=0, antialiased=True
)
ax.set_xlabel("Days to Expiration")
ax.set_ylabel("Strike Price")
ax.set_zlabel("Implied Volatility")
ax.set_title("SPY Volatility Surface")
ax.view_init(elev=20, azim=45)
plt.tight_layout()
plt.show()
Now we can run the main function to generate the volatility surface.
def volsurface():
# Get market data
risk_free_rate, historical_price, current_price = get_current_market_data()
print(f"Using current price: {current_price}")
# Load and process calls data
calls = pd.read_csv(OPTIONS_CSV)
calls["t"] = calls["daysToExpiration"] / 365.0
# Calculate historical volatility
sigma = historical_price['Close'].pct_change().std() * np.sqrt(252)
# Calculate implied volatilities
calls["calculated_iv"] = calls.apply(
lambda row: calculate_iv(row, risk_free_rate, sigma), axis=1
)
calls = calls.dropna(subset=["calculated_iv"])
# Create and plot surface
X_new, Y_new, Z_smooth = create_volatility_surface(calls)
plot_volatility_surface(X_new, Y_new, Z_smooth)
Volatility Arbitrage
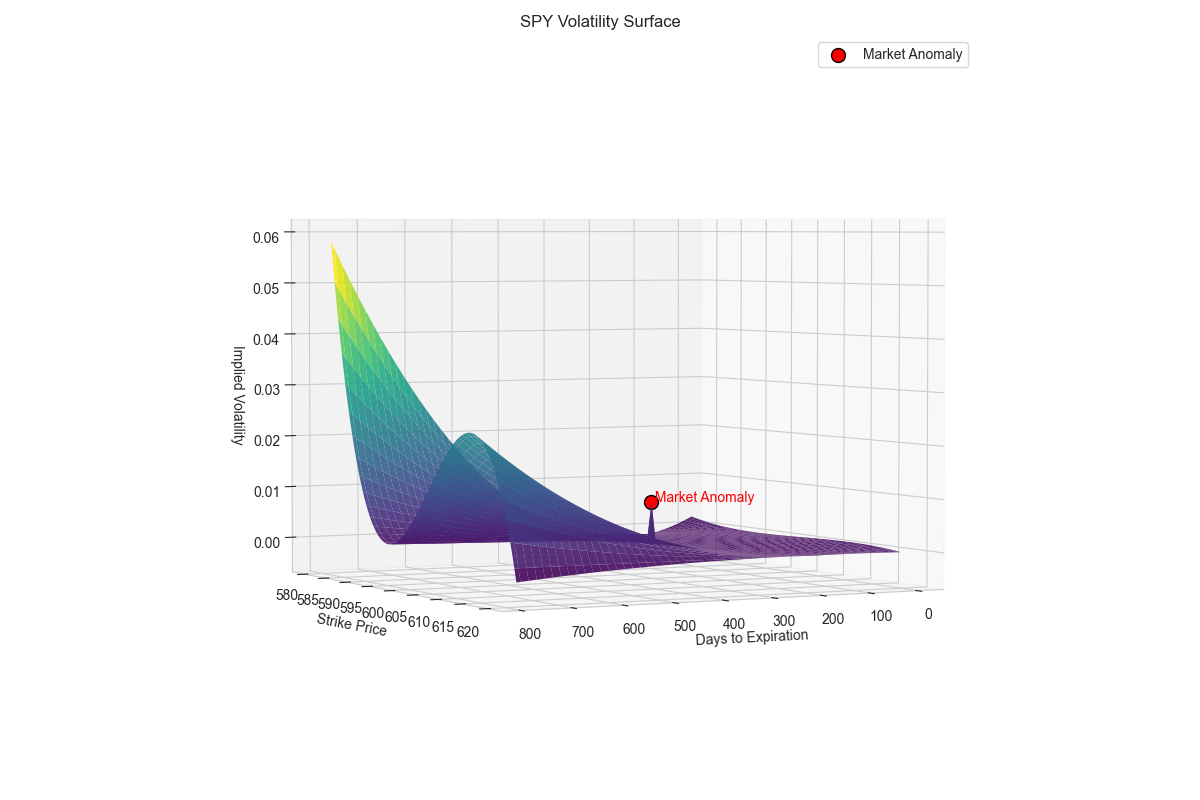
The surface shows the market's expectation of future volatility across different strikes and expirations. When there are irregularities or "bumps" in the surface, it may indicate mispriced options. This is a type of trading strategy called volatility arbitrage. We're essentially bet on whether the market's expectations of how much a stock's price will move are too high or too low. Basically, you're trying to profit from the difference between what the market predicts for future volatility and what you believe it will actually be.
We can identify areas where the market has mispriced options by looking for areas where the volatility changes abruptly as compared to the surrounding areas by calculating the gradient of the surface and looking for areas where the gradient is greater than a certain threshold.
# Find areas where volatility changes abruptly
def find_vol_arbitrage(surface, threshold=0.02):
vol_gradients = np.gradient(surface)
anomalies = np.where(abs(vol_gradients) > threshold)
return anomalies
If we were to find a inefficiencies in the surface, we could then buy the underpriced option, sell the overpriced option and delta hedge with the underlying asset for a guaranteed profit. Of course, finding inefficiencies is not easy and requires a lot of work. For options on assets like SPY, the market is very efficient and thousands of other people are trying to find inefficiencies at near nanosecond speeds so your probability of success is very low.
Skew Trading
The volatility skew refers to the difference in implied volatility between out-of-the-money options, at-the-money options, and in-the-money options. Skew trading involves exploiting the discrepancies in implied volatilities across different option strikes. Traders analyze the skew to identify mispriced options and implement strategies that can profit from the expected normalization of these discrepancies.
The volatility "smile" is a convex pattern in the volatility surface where implied volatilities are higher for both in-the-money ITM and OTM options compared to ATM options. This convexity, shaped like a smile or smirk when plotted, indicates that market participants are willing to pay more for options that are away from the current market price. The convex shape emerges because traders often seek protection against both upside and downside risks - buying OTM puts to hedge against market crashes and OTM calls to capture potential rallies. This behavior directly relates to our earlier discussion of volatility arbitrage, as the smile pattern can create opportunities for traders to exploit any temporary distortions in this typically stable relationship.
A volatility smile is symmetric, with higher implied volatilities for both OTM puts and OTM calls compared to ATM options.
A volatility smirk is asymmetric, with higher implied volatilities for OTM puts compared to OTM calls.
Think of skew trading like betting on the market's fear levels evening out. When traders get really worried about market crashes, they drive up the prices of "insurance" (put options) compared to "lottery tickets" (call options). This creates a lopsided or "skewed" pattern in option prices. Skew traders try to make money by betting that this fear will either increase or decrease - they might buy the relatively cheap calls and sell the expensive puts if they think the market is being too paranoid, or do the opposite if they think people aren't worried enough. It's like being a fear arbitrageur, profiting when market psychology swings between extremes of panic and complacency.
We can analyze the skew by performing a linear regression on the IV vs strike and looking for a trend.
def analyze_volatility_skew(options_data):
# Filter ATM options
atm_strike = options_data.iloc[(options_data['strike'] - options_data['lastPrice']).abs().argsort()[:1]]['strike'].values[0]
# Calculate skew: IV vs Strike
skew_data = options_data.copy()
skew_data['strike_diff'] = skew_data['strike'] - atm_strike
skew_data = skew_data[~skew_data['impliedVolatility'].isna()]
# Perform linear regression to quantify skew
slope, intercept, r_value, p_value, std_err = linregress(skew_data['strike_diff'], skew_data['impliedVolatility'])
print(f"Skew Slope: {slope:.5f}, R-squared: {r_value**2:.5f}")
# Plot the skew
plt.figure(figsize=(10, 6))
plt.scatter(skew_data['strike_diff'], skew_data['impliedVolatility'], label='Options')
plt.plot(skew_data['strike_diff'], intercept + slope * skew_data['strike_diff'], 'r', label='Linear Fit')
plt.xlabel('Strike Difference (Strike - ATM Strike)')
plt.ylabel('Implied Volatility')
plt.title('Volatility Skew Analysis')
plt.legend()
plt.show()
return slope